Considerações sobre a Incerteza
Alberto Mesquita Filho
Capítulos 9 a 11 do Livro
Confesso Que Blefei
Física Antiga x Moderna
©1987
1 — Nem tudo o que reluz é ouro
Você sabe quanto custa um quilo de feijão? Ótimo! Calcule então o preço de um grão de feijão e... Oh! É verdade! Não é tão simples assim. Primeiro precisamos saber quantos grãos existem em um quilo. Pois saiba que se você contar o número de grãos em vários sacos de um quilo, notará uma certa diferença entre um e outro; mesmo admitindo-se a honestidade do dono do supermercado. Heim?... Como é que eu sei isso? Ora, você é mesmo um incrédulo. Pois eu... Bah! Pois faça você a experiência e se eu estiver errado não deixe de me avisar a tempo de corrigir este item para a próxima edição. Mas garanto que a sua incredulidade vai custar caro. O preço mínimo é o de dois quilos de feijão. Quanto mais dinheiro você dispuser, melhor. Mas o dinheiro não é tudo. Antes de comprar o feijão lembre-se de que existe uma lei: o quanto você vai gastar é diretamente proporcional a sua paciência em contar os grãos.
Esta lei apóia-se numa regra metodológica: o cientista não deve ser esbanjador, mesmo que o dinheiro seja seu. Por incrível que pareça, poucos conhecem esta regra; mesmo porque quase sempre o dinheiro é do Estado, ou melhor, do povo. Entendidos a lei e a regra, mãos à obra. Ou melhor, mão na carteira.
Se o seu coeficiente de proporcionalidade for bastante grande, você conseguirá contar os grãos contidos em uns 100 sacos de 1 quilo. Não me pergunte onde arranjar dinheiro para isso. Acima disso, só mesmo o Eratóstenes ou o Jó. Não só pela paciência mas também porque naquela época a economia era mais estável.
Com os 100 valores obtidos você poderá tirar a média: o resultado será o número médio de grãos por saco. Divida o preço de um quilo por este valor e você obterá o procurado.
Viu como é simples! E já que o processo é simples, você poderá repeti-lo para grãos de arroz, de milho, etc. E assim você adquirirá o importante conceito que diz: Nem tudo o que enche o saco é feijão. É uma outra maneira de dizer "nem tudo o que reluz é ouro" ou, então, "nem tudo o que se curva é uma onda".
Após ter calculado o preço de um grão de feijão você concluirá que é um felizardo. Se ainda não concluiu, calcule quantos grãos de feijão por dia pode comer um pobre coitado que ganha o salário mínimo. Concorda comigo agora?
Procure valorizar o dinheiro empatado e aproveite o mais possível o seu trabalho. Não despreze os 100 valores obtidos. Construa, por exemplo, um histograma (isto se você possuir conhecimentos elementares de estatística) e verifique quanto ele se aproxima de uma curva de Gauss.
Admitindo que você tenha guardado os grãos de feijão nos mesmos sacos... Ops! Desculpe, isso era importante mas eu esqueci de avisar. ...ou seja, que cada um ainda seja de um quilo, você poderá constatar o que eu chamaria uma ilusão de óptica: dois sacos aparentemente iguais têm números diferentes de grãos.
Agora faça uma feijoada e bom apetite. Distribua o feijão restante entre seres menos felizardos do que você. Não vai alterar em quase nada a fome no mundo mas deixará a sua consciência mais leve. E a minha também.
Um sistema homogêneo é aquele que tem as mesmas propriedades em todos os seus pontos. A rigor não existe. Isto se dermos uma conotação matemática para os pontos. Os espaços em branco de uma folha de papel parecem trechos homogêneos; são iguais em todos os seus pontos; mas esta igualdade não resistirá a um exame mais detalhado com uma lupa de médio aumento.
Essa não existência não chega a preocupar muito os químicos. Mesmo porque as propriedades a que se referem não são pontuais e englobam um espaço mínimo. Ou seja, o que um químico diz ser um sistema homogêneo é, na realidade, um conjunto de sistemas micro-heterogêneos agrupados de maneira a simular um produto dotado de partes macroscopicamente semelhantes.
As propriedades de estado de um sistema são "os atributos físicos percebidos pelos sentidos ou tornados perceptíveis pelos métodos experimentais de investigação". A concentração em açúcar de uma solução aquosa pode ser estimada pelo paladar e é, portanto, uma propriedade da solução. Uma solução de açúcar em água é uma solução homogênea; a concentração é a mesma em todos os "pontos" da solução. No entanto, se restringirmos estes pontos a algo bem pequeno, por exemplo o espaço ocupado por umas mil moléculas de água, chegaremos à conclusão de que em muitos destes "pontos" não existe molécula alguma de açúcar e que, a este nível, o sistema é heterogêneo.
O conceito químico de homogeneidade pode ser expandido para sistemas maiores; é suficiente aumentar o objeto de estudo e, ao mesmo tempo, aumentar o espaço mínimo de interesse, ou seja, o que consideramos como "pontos". Os astrônomos consideram o Universo homogêneo; tão homogêneo quanto uma solução de açúcar em água. Nestas dimensões, o sistema solar é muito menor do que um ponto astronômico. Somos menos que um ponto no Universo Cósmico!
No item anterior estudamos sacos de feijão; e admitimo-los homogêneos. Ao calcular o preço de um grão de feijão desprezamos o espaço existente entre os grãos. Este espaço foi considerado como algo sem preço, uma oferta da casa. Os sacos tinham algo em comum: eram todos de um quilo ou um quilograma. A massa gravitacional é fornecida por uma balança e é uma propriedade de estado; está intimamente relacionada à sensação subjetiva de peso.
A sensação é sempre um dado subjetivo. Podemos dizer que dois objetos têm o mesmo peso e outra pessoa nos contestar, achando que um é mais pesado do que o outro. A balança desfaz esta subjetividade. Mas as balanças também são imperfeitas. Ainda que em menor grau, também nos enganam. Os motivos são vários, não cabendo aqui discuti-los. Mas convém que conheçamos algo muito importante, ainda que de forma rudimentar ou meramente conceitual. Refiro-me à precisão e à exatidão de um instrumento ou de uma medida.
Se você julga que encontrou exatamente o valor pago por um grão de feijão, pelo simples fato de "ter contado" 100 quilos de grãos, você está redondamente enganado. E o seu engano terá sido tanto maior quanto menor tiver sido o rigorismo da empresa que pesou os sacos; e isto inclui a balança utilizada. Em ciência, honestidade não é tudo, ainda que fundamental. Não tenha dúvida que alguns sacos tinham mais do que 1 quilo e outros menos.
Você já viu uma balança? Se ao invés de pesarmos 100 sacos nós pesarmos o mesmo saco 100 vezes... Obteremos o mesmo resultado? Certamente não. Diz-se que uma balança é tanto mais precisa ou fidedigna quanto mais próximos ou agrupados estiverem estes 100 valores. Mas agrupados em torno de que valor? Por outro lado: uma balança é tanto mais exata quanto mais a média obtida em várias pesagens aproximar-se dos padrões clássicos de medida.
É comum a referência ao tiro ao alvo na explicação de exatidão e precisão. Admitamos que você possua uma arma e um alvo; e quer testar a precisão da primeira. Um fabricante de armas iria procurar um mecanismo de disparo que não influenciasse o tiro. Mas como queremos apenas conceituar a precisão, não é necessário tantos cuidados. Admita apenas que você é um bom atirador, o que eliminará grande parte da subjetividade dos resultados; e também fará bem ao seu "ego".
Mas não leve isto muito a sério. Lembre-se: as armas foram criadas para facilitar a vida do homem; ou para que um físico pudesse estudar balística; ou ainda para que você praticasse um esporte. Posteriormente à criação, alguém que não tinha nada a ver com a invenção percebeu que ela servia para matar seus semelhantes; e terceiros perceberam que poderiam se enriquecer aproveitando-se desta falha humana. E passaram a propalar a violência e a ensinar o homem a se defender da violência com a violência. E, ao mesmo tempo, passaram a fabricar em série o agente desta insensatez. Conseguiram, desta forma, e impunemente, poderio e riqueza. E passaram a dirigir os destinos do mundo e, consequentemente, do homem. E a esta hora estão rindo de mim e de você e de todos aqueles que acreditam numa reviravolta... sem violência.
Sendo você um bom atirador e mirando o alvo corretamente, após uns quatro ou cinco tiros será capaz de afirmar se a arma é ou não de boa precisão. Veja que não é necessário acertar o alvo para isso; e nem mesmo aproximar-se do ponto central. Se todos os pontos atingidos estiverem deslocados, digamos, para cima e para a direita de onde você mira, mas bem agrupados, não tenha dúvidas: a sua arma é bem precisa, embora possa não ter exatidão equivalente. Sendo você um bom atirador, certamente saberá corrigir esta falha; é suficiente mirar um pouco para baixo e para a esquerda do ponto central nos próximos tiros. Note que não é apenas a arma que está sendo examinada: você também. E ainda que preciso, você poderá ser inexato se possuir vícios de posição, ou outros. Se você apresentar tremores, os tiros serão desviados ora num, ora noutro sentido; e a sua precisão deixará bastante a desejar.
Um aparelho de medida pode ser de alta precisão e bastante inexato ou vice-versa. E este é um dos pontos em que a estatística auxilia o cientista. Com o tempo você irá se familiarizando com os aparelhos de medida que usa. E notará que a paciência é fundamental mas que a sabedoria às vezes lhe indica caminhos mais curtos.
4 — Consertando os erros
A essa altura você quer saber se a balança da empresa que efetuou as pesagens é exata. A precisão não lhe preocupa muito, pois a experiência foi feita 100 vezes. Pois saiba que, mesmo não sendo a balança muito exata, você pode consertar o erro; é suficiente contar com outra balança e, esta sim, de alta exatidão; e calcular o fator de erro, deslocando, desta forma, a sua média deste valor. Nunca jogue fora os resultados de uma experiência bem conduzida. Há sempre uma saída para recuperar um tempo aparentemente perdido.
Há, no entanto, um detalhe que não pode ser de maneira alguma esquecido: Na experiência citada não foram feitas determinações de pesos individuais e sim de uma população de grãos de feijão, qual seja, a população contida em sacos de 1kg. Não obstante, o valor que nos interessava calcular refere-se a "um" indivíduo, ou seja, o preço de "um" grão de feijão. Seria possível calcular este valor sem margem de erro admitindo-se uma balança 100% precisa? Esta balança não existe mas, mesmo que existisse, a resposta somente seria afirmativa para uma população homogênea. Caso contrário persistiria um fator de incerteza na determinação do peso de um grão de feijão; mesmo que você tenha contado o número exato dos mesmos. Vejamos o porquê.
Tome um punhado de grãos de feijão e reuna-os em cima da mesa. Observe bem os seus caracteres: tamanho, forma, irregularidades, etc. Você acabará concluindo que a população é heterogênea quanto ao peso; e que, obviamente, os mais pesados contribuíram mais para o peso da população e, portanto, custaram mais caros do que os mais leves. Concluirá ainda que o preço que você determinou para um grão de feijão nada mais é do que um valor médio para a população. E concluirá, também, que se você aplicar este valor médio para um determinado grão estará cometendo sempre um erro, por menor que seja; o valor real deste grão específico estará dentro de uma faixa que vai desde o valor do mais barato (ou o mais leve) até o do mais caro (ou o mais pesado). A esse intervalo chamaremos incerteza (caso fosse conveniente, eu poderia também definir a incerteza como um valor proporcional a esse intervalo, por exemplo, 70% do mesmo).
Note que é impossível reduzir esta incerteza por um método que estude populações. O que não significa, em hipótese alguma, que não se possa utilizar métodos individuais, com o que a incerteza desaparece, restando apenas os caracteres precisão e exatidão. E estes podem ser reduzidos com a melhoria das condições experimentais.
Podemos então enunciar o que chamarei "Teorema da Indeterminação":
Ao se estudar uma população heterogênea pela utilização de propriedades populacionais (e não individuais) os valores individuais obtidos estarão sempre sujeitos a um fator de incerteza independente da precisão e/ou exatidão do método e dependente do grau de heterogeneidade da população em estudo.Trata-se de um teorema tão óbvio quanto desconhecido.
1 — A Incerteza de Heisenberg
Não é muito comum o estudo da incerteza em ciências naturais. Um dos poucos campos que a leva em consideração é a física moderna. Começou a ser valorizada a partir dos trabalhos de Werner Heisenberg (1927), passando a ocupar um papel de destaque. Chegou mesmo a se transformar num dos pilares da mecânica quântica através do que foi chamado Princípio da Incerteza ou da Indeterminação. E este chegou a ser o gerador da maioria dos temas polêmicos da física de nosso século. Em algumas versões atuais da física quântica é encarado como princípio; em outras como consequência. E, ao que parece, grande parte dos físicos pertencentes à chamada linha realista admite a possibilidade do descobrimento de variáveis ocultas que, uma vez identificadas, transformariam o estudo da física das partículas elementares em algo concreto, concebível, racional e não apenas lógico.
Em 1927 Heisenberg percebeu uma limitação fundamental na exatidão com que se pode determinar simultaneamente a posição e a velocidade de uma partícula microscópica. Vejam que não é uma incerteza simples, como a que vimos no capítulo anterior (Homogeneidade e Incerteza). Em teoria, a posição poderia ser determinada de forma exata e precisa; e o mesmo se diga para a velocidade. A impossibilidade residia na determinação conjunta dos valores.
A conclusão era desalentadora. Era um empecilho para o estudo das partículas elementares, encontrado justamente quando tudo parecia estar se tornando claro. Ainda se regozijavam os físicos com as recentes descobertas do elétron (Thompson), do núcleo atômico (Rutherford), da estrutura atômica (Bohr), etc. Ao que tudo indicava, dez ou vinte anos seriam suficientes para a decifração da maioria dos enigmas relacionados à estrutura da matéria. E de repente surgia um princípio, ou uma consequência de outros princípios, a dizer: "cessa tudo quanto a antiga musa canta; outro valor mais alto se alevanta". Chegara a hora de começar tudo de novo e quase da estaca zero.
2 — A Física das Probabilidades
Se o leitor não conseguiu entender a importância da determinação simultânea da posição e da velocidade, um exemplo simples poderá convencê-lo. Imagine um automóvel numa estrada entre as cidades A e B. Conhecendo a posição e a velocidade num determinado instante ser-lhe-á possível estimar a hora da chegada, digamos em B. Conhecendo apenas a posição ou apenas a velocidade, o tempo da chegada estará indeterminado.
No caso de partículas a situação é ainda mais drástica pois a estrada não é conhecida; ou seja, uma partícula move-se num espaço tridimensional e quando dizemos velocidade estamos nos referindo não apenas a um trajeto percorrido em determinado tempo mas também à direção e ao sentido (ou seja, a trajetória a percorrer, isto é, a estrada). Então, ao determinarmos exatamente a posição de uma partícula, e sendo o princípio da incerteza verdadeiro, não poderemos saber quase mais nada sobre a partícula.
Entendam que a matéria é formada por partículas elementares; e estas movem-se intensamente. Se conseguirmos localizar a posição de uma partícula em relação a outra, não poderemos dizer como ela se move; sequer saberemos a trajetória mas apenas um ponto desta. Por outro lado, se conhecermos o movimento num dado instante, não saberemos onde ela se localiza e portanto não teremos dados completos sobre a trajetória. E o que o princípio da incerteza retrata é nada mais do que: É impossível conhecer a estrutura íntima da matéria, pois é impossível saber como as partículas elementares se interagem.
Ao mesmo tempo que Heisenberg convencia-se desta impossibilidade, a mecânica quântica estava começando a adquirir raízes sólidas, principalmente através dos estudos de Erwin Schrödinger. Apoiava-se em outros temas também polêmicos como os "quanta" de Planck, o efeito fotoelétrico de Einstein, a constância da velocidade da luz de Einstein, a dualidade corpúsculo-onda de De Broglie, etc. Matematicamente, a física estava dando um grande salto, ainda que bastante confuso. Mas, desgraçadamente, Schrödinger estava, e acredito que para sua surpresa, conseguindo provar que Heisenberg estava com a razão. Por vias totalmente diversas chegara a conclusões praticamente semelhantes.
O curioso é que Heisenberg aceitara, pelo menos em seu raciocínio inicial, as partículas como sendo corpúsculos; e Schrödinger partira da teoria ondulatória ou, mais precisamente, da dualidade corpúsculo-onda. Por outro lado, a teoria de Heisenberg era individual e a de Schrödinger populacional. E as duas nos levavam a uma incerteza. Numa delas como princípio; na outra como consequência.
As coincidências eram tantas que o absurdo se fortaleceu. E quem teve a ganhar com isso foi a física de Schrödinger e por dois motivos. Em primeiro lugar, a incerteza em teorias populacionais é algo esperado, como vimos no capítulo anterior, desde que as populações sejam heterogêneas; e, portanto, a teoria de Schrödinger não passaria por uma crítica rigorosa que questionasse a identidade de partículas aparentemente semelhantes. E, por outro lado, se como Heisenberg demonstrou, é impossível estudar o movimento de uma partícula, nada melhor que se contentar em estudar um conjunto de partículas. E as idéias de Schrödinger estavam abrindo as portas para isso.
As vozes que surgiram contra foram abafadas. Nem mesmo os mitos escaparam. Se até mesmo Aristóteles e Newton houveram sido "derrubados", porque dar ouvidos à razão quando a "lógica" se impõe? E Einstein ficou falando sozinho, ou quase sozinho; e até mesmo ridicularizado por uma frase que "deixou escapar":
— "Não posso acreditar que Deus seja um jogador de dados."Curiosamente, Einstein foi um dos pais da física que o derrubou: a física das probabilidades.
Os elétrons são partículas muito pequenas que entram na constituição dos átomos de Dalton. Existem outras menores, como os fótons e os neutrinos, e maiores, como os prótons e os nêutrons. As demais, como aquelas que costumeiramente aparecem nas manchetes científicas dos jornais, são terrivelmente instáveis e raramente nos incomodam. Em geral, são produzidas artificialmente em fantásticos laboratórios sobrenaturais.
Muitas são as maneiras pelas quais podemos "desconfiar" da existência dos elétrons. Em geral, estão relacionadas aos efeitos elétricos (ou de uma carga elétrica) ou magnéticos (ou de uma corrente elétrica). Porém, o que "enxergamos" são agrupamentos de elétrons pois nenhuma das cinco partículas citadas são individualizadas pelos métodos comuns de investigação; pelo menos até que alguém consiga dar uma interpretação dialética para o que conceituamos como "métodos comuns"; e é o que foi feito por Wilson.
A neblina é um fenômeno comum e que nos atrapalha bastante se estivermos na direção de um automóvel. Enxergamos o que não queremos ver: um agrupamento imenso de partículas atmosféricas que, indiferentes a nossas preces, recusam-se a sair de nossa frente. Pois a câmara de Wilson utiliza-se do fenômeno neblina de uma forma bastante genial. Seu princípio é bastante simples; e o instrumento é, em essência, uma câmara de expansão, sob certos aspectos semelhante a uma seringa de injeção.
Sabe-se que a quantidade de água que se dissolve no ar que nos envolve, ou em um gás qualquer, é muito variável. Em certas condições, como por exemplo, uma diminuição brusca de pressão, o ar torna-se supersaturado, ou seja, com mais moléculas de água do que comportaria em condições normais de obediência às leis simples de diluição; até aí não temos neblina. Acontece que este equilíbrio é instável. Apesar de instável, a situação é de equilíbrio e, portanto, pelo menos em teoria, poderia ter uma duração infinita, desde que nada ocorresse no sistema que o perturbasse a ponto de provocar a precipitação das moléculas de água. Mas... O que perturba a situação? Muitas coisas a que chamamos irregularidades e que, em geral, estão relacionadas a partículas que trafegam por este meio.
Uma irregularidade "local" serve como núcleo inicial para a condensação de moléculas do vapor de água supersaturado, em gotículas de água. Se as irregularidades forem muitas, teremos a neblina. Se o gás da câmara for bastante limpo, sem poeiras, as trajetórias de partículas, que porventura penetrem na câmara, serão delineadas, podendo ser fotografadas; especialmente se o sistema for dotado de um contador Geiger que, ao "notar" a presença da partícula, dispara a máquina fotográfica num tempo em que a neblina é apenas local. Pode-se, assim, estudar a trajetória e consequentemente o movimento de partículas elementares. Pode-se também estudar os efeitos de um campo elétrico ou magnético sobre a trajetória das partículas. É suficiente colocar a câmara de Wilson num local onde existam estes campos, como nas proximidades de uma carga elétrica ou de um imã. E às vezes são justamente estes efeitos que identificam a partícula em estudo.
4 — A Lógica de Heisenberg
Ao que parece Heisenberg estava preocupado com o estudo da trajetória de partículas elementares, como o elétron, em câmaras especiais, como a de Wilson. Os elétrons são partículas muito pequenas, não sendo possível visualizá-los; mas em tais câmaras, como vimos, deixam um rastro, graças à modificação das características das moléculas do meio atravessado. E estas últimas, ou mesmo agrupamentos destas, tornam-se visíveis. O que se vê é, no entanto, muito maior do que o elétron. Podemos, por este método, delimitar uma região ocupada pelo mesmo; mas nunca determinar exatamente a posição do elétron.
A este ponto Heisenberg passou a tecer considerações teóricas. E a penetrar no campo das experiências imaginárias, utilizando-se da lógica transcendental. E o fez com sabedoria e, portanto, sem ferir normas nem preceitos científicos. Seu método é genuíno e válido, e utilizado há milênios. Vamos tentar reproduzir seu raciocínio.
Admitamos a possibilidade da existência de um meio dotado de partículas menores do que as moléculas utilizadas na prática; ou seja, menores do que as moléculas de água da câmara de neblina mas que, apesar disso, nos permitam uma experiência semelhante. Fosse isso possível, seria de se esperar que a região perturbada se tornasse menor. E, com isto, a precisão do método seria aumentada. Como estamos no terreno das experiências imaginárias, podemos reduzir o tamanho das moléculas do quanto quisermos. E em teoria, e à primeira vista, localizar exatamente a posição do elétron no limite em que o tamanho das moléculas "fosse igual a zero".
Não estranhem este método. Não há nada de errado com ele enquanto nos lembrarmos que estamos num terreno imaginário. E, além do mais, a lógica transcendental não lhe dá respostas imediatas, mesmo porque elas seriam absurdas. Trata-se de um método científico de raciocínio porém quase que puramente filosófico. É mais uma tentativa de antecipar o que aconteceria se a experiência conseguisse atingir este nível refinado, hipotético, utópico, irrealizável mas, acima de tudo, maravilhosamente ideal. Trata-se de um limite físico que não difere conceitualmente do limite matemático; e o limite matemático nos leva a algo concreto, como a determinação de uma área, um volume, etc.
Porém Heisenberg notou, e muito sabiamente, que um novo problema surgiria se adotasse esta linha de conduta. Ao reduzir o tamanho da "isca", ou seja, das moléculas do meio, torná-las-ia menos resistentes aos impactos com a "pesca", ou seja, os elétrons. E quanto menor fosse a partícula de prova, mais longe ela seria lançada após o choque ou interação com os elétrons. E se, de alguma maneira, conseguisse "enxergar" esta partícula, ela não estaria exatamente na posição por onde passou o elétron mas afastada de um valor tanto maior quanto menor o seu tamanho ou, melhor, a sua massa. Ocorreria, então, um tipo de incerteza diferente do visto no capítulo anterior, pois estamos nos referindo ao estudo da posição de um único elétron e não da média da posição de muitos elétrons. Trata-se de uma impossibilidade ou indeterminação inerente ao método; e o método estuda a trajetória de uma única partícula que se choca com outras.
Qualquer tentativa de melhorar a precisão do método nos levará a uma melhora na medida da quantidade de movimento da partícula: Produziremos uma melhora nas condições de estudo do espalhamento que a mesma produz no meio e, consequentemente, no estudo de sua massa e/ou velocidade pois quanto maiores forem estas duas em relação às partículas do meio, maior será o espalhamento. Mas prejudicamos, com isso, o estudo da posição. E agora podemos enunciar o princípio de Heisenberg na sua versão mais simples, ou seja, o princípio da incerteza da posição-momento:
É impossível conhecer simultaneamente e com exatidão a posição e o momento de uma partícula.Por momento entenda-se o produto da massa pela velocidade.
5 — Um microscópio refinado
Ao estudarmos a trajetória do elétron numa câmara de neblina, de alguma forma captamos sua imagem. Ou seja, existe uma terceira entidade não considerada no item anterior: a luz. O que obtemos na câmara de Wilson é a "imagem da imagem" do elétron. A luz colabora neste caso para com pequena parte do que chamamos incerteza do método.
Podemos refinar um pouco a "pescaria". A "pesca" continuará sendo o elétron; mas a isca será agora única e exclusivamente um feixe de luz. Desta forma, abandonamos as partículas da câmara de Wilson responsáveis pelo fenômeno neblina. Na realidade, abandonamos a própria câmara. Nestas condições não é necessário nem mesmo o lançamento de elétrons: estes podem estar em movimentos vários e até mesmo próximos do repouso. Os corpúsculos lançados agora são os fótons.
A experiência é imaginária e também limite. Estamos imaginando um microscópio óptico que "ainda" não existe e vale a pena tecer algumas considerações sobre o que foi dito em capítulos anteriores. A luz sofre "difração" ou inflexão de seus raios ao passar por um orifício. Pois o que é um corpúsculo se não o antagônico complementar de um orifício de mesmo tamanho? Graças à simetria verificada entre os fenômenos naturais, deve ocorrer uma inflexão invertida quando a luz passa por um corpúsculo. Aliás, nem precisaríamos pensar nesta simetria se nos lembrarmos da inflexão sofrida por feixes de luz que passam próximos à borda superior de um anteparo.
Graças à inflexão da luz os microscópios ópticos têm um poder de resolução limitado: ao tentarmos aumentar a ampliação encontramos um limite a partir do qual a imagem de um corpúsculo aparece borrada e, consequentemente, pouco nítida. Para cada microscópio, e na dependência de sua configuração, e ainda, para cada tipo de luz utilizada, este limite é diferente. E a menor estrutura que pode ser analisada claramente por um microscópio específico deve ter um tamanho determinável pelas leis da óptica geométrica associadas às chamadas leis da "difração". Pelo menos em teoria podemos imaginar um microscópio óptico com poder de resolução da ordem das dimensões de um elétron. Trata-se de mais uma aplicação sutil da lógica transcendental. E de mais um limite físico.
Mas se disse em teoria, disse-o bem. Pois na prática a teoria é outra, como teria dito o crítico economista Joelmir Beting; ou melhor, na prática devemos pensar em todas as teorias envolvidas e concomitantemente compatíveis com a lógica utilizada. E sabemos que fótons e elétrons se interagem; e trocam movimentos. E quando enxergamos um elétron em várias posições consecutivas, sabemos de onde ele vem, mas não sabemos para onde ele vai; pois o último fóton que se chocou com ele, e que nos fornece a última imagem, alterou o seu movimento e de uma forma que, a serem verdadeiras as leis da "difração", não sabemos de quanto, em que direção e em que sentido. Conhecemos o passado do elétron mas não o seu futuro. E, em se tratando de uma experiência imaginária, talvez nem mesmo o seu passado, pois a teoria quântica "não permite" uma determinação tão rigorosa e contínua da trajetória: o elétron deverá aparecer saltitando, ora num lugar, ora noutro, mostrando-se como corpúsculo à medida que os "quanta" de luz atingem nossos olhos e como "onda" nos intervalos.
6 — A Contribuição de Bohr
Ao que parece, a idéia do microscópio óptico foi de Heisenberg; mas quem melhor soube explorar as vantagens das sutis mudanças de referencial foi Niels Bohr. Seu maior mérito foi conseguir de uma maneira simples e utilizando-se das expressões mais elementares e diretas que apóiam a teoria quântica, quantificar a incerteza de Heisenberg. Aliás, parece não haver campo da física moderna, ou até mesmo da clássica, onde Bohr não tenha dado contribuições importantes deste tipo. Sempre conseguiu, de alguma forma, enxergar mais longe que seus colegas.
Bohr transcendeu a experiência do microscópio a um outro limite. Admitiu a possibilidade de localizar o elétron com um único fóton, ou seja, com um "quanta" de luz, a menor fração de luz de um dado "comprimento de onda". Este fóton seria "espalhado", ou "dispersado", pelo elétron, em concordância com as leis da "difração". Chama-se "espalhamento" porque "não podemos" determinar a direção exata mas, apenas, conhecer as direções mais prováveis. E é esta probabilidade que é estimada pelas leis da "difração".
Conhecendo os desvios mais prováveis, podemos calcular as variações mais prováveis do que os físicos chamam "momento de um fóton" (momento = p = quantidade de movimento). É suficiente utilizar as relações de Einstein-De Broglie. Obtém-se, assim, o intervalo probabilístico Δp para o momento do fóton. Δp é, portanto, a incerteza na determinação da quantidade de movimento do fóton após a interação. E como fóton e elétron trocam movimentos, o Δp do elétron deve ter o mesmo valor absoluto.
Por outro lado, como a luz se "difrata", o fóton nos mostra uma posição diferente daquela onde realmente se encontra o elétron. É possível, utilizando-se também as leis da "difração", calcular a incerteza da posição (Δx) do elétron.
Por uma "feliz" coincidência, ao multiplicarmos Δx por Δp, obtidos como acima comentado, uma série de fatores se cancelam e chegamos à expressão:
Δp×Δx = h/4π,
em que h é a chamada constante de Planck.
Se conhecermos o valor exato da posição (x) ou do momento (p), as variáveis Δx ou Δp (uma ou outra) deverão ser iguais a zero; ou seja, conhecendo um valor exato, a incerteza não existe para a grandeza considerada. Porém, se Δx ou Δp for igual a zero, a outra variável (Δp ou Δx) deverá ser infinita, em concordância com a fórmula deduzida. Ora, um valor infinito para o desvio significa que sequer podemos estimá-lo.
As melhoras na exatidão da determinação de uma ou de outra grandeza podem ser fisicamente tentadas. Mas ao melhorar uma, prejudicamos a determinação da outra. É o que nos diz o princípio; e é o que nos diz a fórmula. Fisicamente, "podemos" melhorar a estimativa de Δx usando luz de pequenos "comprimentos de onda"; e Δp, usando luz de grandes "comprimentos de onda". Heisenberg, como vimos, havia chegado à mesma conclusão utilizando-se apenas do raciocínio lógico, sem lançar mão de equações.
A constante de Planck é considerada uma das mais importantes constantes da física. Aparece em inúmeras situações em que a interpretação de um fenômeno suscita a dedução de uma "lei" direta ou indiretamente relacionada à luz.
A dedução de Bohr engrandeceu sobremaneira a confiabilidade na teoria quântica. Embora tenha derrubado um princípio, pois mostrou-o ser consequência de leis, Bohr chegou de uma maneira não apenas lógica, mas também racional, a uma das previsões quantitativas da teoria de Schrödinger.
1 — Introdução
Existe um princípio oriental que diz que tudo o que existe no Universo pode ser encarado como constituído por antagônicos complementares, ou seja, o que chamam de yin e yang [1]. Se o princípio for verdadeiro deveremos encontrar, na física moderna, o antagônico complementar da incerteza: a certeza. É claro que ela deverá estar sempre acompanhada de outras incertezas mas, de qualquer forma, creio que é melhor estudar o certo do que o incerto.
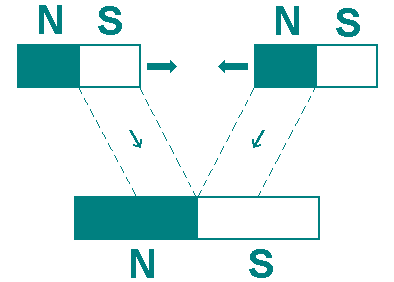
Existe um outro princípio oriental que diz: No extremo, yin transforma-se em yang [2]. Ou seja, se você aproximar o pólo sul de um imã ao pólo norte de outro (figura abaixo), no extremo da aproximação os dois imãs transformam-se num só. O que era pólo sul de um imã passa a ser parte do pólo norte; e o que era pólo norte do outro, passa a ser pólo sul. A mudança se dá apenas nos pólos que entram em contato.
Se este segundo princípio oriental for verdadeiro, não apenas para o magnetismo, no extremo da incerteza devemos encontrar a certeza. E, pelo visto, a física já atingiu este extremo. E eu também já devo ter cansado o leitor com este tema e breve mudarei de assunto. Antes que você siga o princípio a risca e ponha todas as minhas considerações na "lixeira". Aguente mais um pouco: o suficiente para que eu tente lhe apresentar a lógica da certeza.
2 — O Apriorismo de Heisenberg
O raciocínio de Heisenberg foi brilhante; e acredito mesmo que ele esteve próximo de dar um passo muito grande em física. Bastava enxergar um "a priori" desnecessário que estava admitindo e a incerteza teria se esfacelado a seus olhos; e ele certamente teria enxergado a verdade. Mas por puro azar a sua física, corpuscular na origem, estava apoiando a outra física: a física dualística. Esta última já nasceu incerta e, portanto, só poderia deduzir uma incerteza. Apesar de incerta, "era a única" em que se apoiar na época. Mas, na realidade, Heisenberg não estava se apoiando na mesma mas apoiando-a. E a satisfação por esta constatação deve ter bloqueado seu raciocínio.
Heisenberg admitiu implicitamente, em sua teoria, que a posição de uma partícula somente podia ser determinada através do choque seguido da observação de propriedades de outra partícula. Acredito que ninguém o criticou por este ângulo pois este "a priori" é aceito, inconscientemente, por quase todos os físicos modernos que estudam partículas. Eliminado este "a priori", este tipo de indeterminação cai por terra.
3 — A Informática Elementar
William Gilbert (1544-1603) pode ser considerado o pai da informática em física. E Newton parece ter sido o primeiro a reconhecer a natureza imaterial do que costumo chamar por informação motora elementar. E como quase todas as grandes idéias de Newton, esta também encontrei na gaveta. Pergunto, então: O que é que passa de uma carga elétrica para a outra quando elas se atraem ou se repelem? E o que é que passa da Terra para uma pedra, quando esta última cai?
Os físicos modernos responderão que no primeiro caso são os fótons virtuais e, no segundo, os grávitons. Mas eles nem sabem o que são fótons reais! Que dizer dos virtuais? E os grávitons são partículas hipotéticas que surgiram para explicar algumas discordâncias de uma física absurda!
Que me perdoem os defensores da moderna eletrodinâmica quântica [o orgulho da física do século XX pelas fantásticas determinações de valores de grandezas abstratas com uma precisão superior a dez casas decimais], mas os seus fótons são tão virtuais que sequer existem. O que existe não tem nada a ver com o fóton, nem com matéria e nem mesmo com energia. E não se diga que ninguém chamou a atenção para este fato:
É inconcebível que a matéria bruta inanimada possa, sem a mediação de alguma coisa, que não é material, atuar sobre e afetar outra matéria sem contato mútuo...
[Isaac Newton]Se admitirmos que é possível localizar um elétron e mesmo quantificar seu movimento única e exclusivamente pelo estudo das informações motoras que ele emite, ou seja, pelo campo de forças que ele gera em sua periferia, ou melhor ainda, pelas interações de Gilbert, não precisaremos mais preocuparmo-nos com a incerteza materialista de Heisenberg. E poderemos prosseguir nosso estudo a procura de incertezas mais racionais.
4 — Um Tiro Certeiro, Porém...
[Este item foi atualizado (1999) afim de adaptar-se à teoria "A equação do elétron e o eletromagnetismo".]
Bohr, como vimos, deduziu a fórmula da incerteza a partir das leis da "difração" e das relações dualísticas de Einstein-De Broglie. A coincidência com a dedução quântica da teoria de Schrödinger não é tão surpreendente quanto à primeira vista possa parecer. Com efeito, é mais um artefato do que uma coincidência. Tanto a teoria de Heisenberg-Bohr quanto a de Schrödinger são matematicamente corretas e ambas apóiam-se nos mesmos absurdos físicos. E, portanto, não poderiam discordar. Simplesmente a teoria de Schrödinger constata um absurdo físico; e a de Heisenberg-Bohr dá uma interpretação física a este absurdo. É importante observar que, a partir de sua teoria, Schrödinger dedicou grande parte de sua vida a procurar por uma maneira de esclarecer este absurdo, enquanto Heisenberg e Bohr contentaram-se em aceitar o "caráter absurdo da natureza".
A incerteza da "difração" não é muito difícil de ser explicada quando relacionada a um "feixe homogêneo de corpúsculos". Trata-se, neste caso, de uma incerteza populacional. Um feixe homogêneo de corpúsculos (um grande número de corpúsculos distribuídos homogeneamente no espaço e viajando paralelamente entre si), ao atingir um orifício não mais se comporta como homogêneo. Assim que anteparo e orifício começam a ser significativos para o estudo do movimento dos corpúsculos, a homogeneidade se desfaz. Os corpúsculos são diferentemente afetados pelas bordas do orifício pois estão diferentemente afastados das mesmas e, portanto, sofrem interações diversas. Após a inflexão temos uma população heterogênea de corpúsculos quanto à direção e, em seu estudo, deve aplicar-se o teorema da indeterminação, visto em "Homogeneidade e Incerteza", parte 5.
Mas,... e no caso da luz? O que é a luz, afinal? Se a luz for composta por corpúsculos, a explicação está dada acima. Onda certamente não é e apoio minhas convicções em trabalho que publiquei recentemente [A equação do elétron e o eletromagnetismo, item 7.1]. Muito provavelmente o que hoje chama-se onda eletromagnética estaria relacionado a algo referido por Newton, algumas vezes, como "o espírito da matéria", numa tentativa de evoluir para uma teoria representacional de campo. A onda eletromagnética seria então um campo mutante e não propriamente uma onda [3]. De qualquer forma, resta decifrarmos o mistério "Luz". Seria a luz apenas este campo mutante; ou em determinados casos este campo seria povoado por corpúsculos emitidos concomitantemente? Haveria matéria na luz? [4] A esse respeito vale a pena reproduzirmos o seguinte texto:
A história da busca de uma teoria da luz não está de modo algum concluída. O veredicto do século XIX não foi final e definitivo. Todo o problema de decidir entre corpúsculos e ondas ainda existe para a Física moderna, desta vez de uma forma muito mais profunda e intrincada. Aceitemos a derrota da teoria corpuscular da luz até reconhecermos a natureza problemática da vitória da teoria ondulatória
[Einstein e Infeld em "A Evolução da Física", Zahar Ed., Rio de Janeiro, 1980, p.98].Resta-nos analisar a complementaridade de Bohr. É óbvio que se a difração existe apenas em fenômenos ondulatórios, como o som, e a inflexão em fenômenos corpusculares como um feixe de elétrons, o princípio da complementaridade de Bohr é tão verdadeiro quanto desnecessário; pelo menos da forma como foi enunciado. A luz, enquanto tal, jamais será observada como som, nem vice-versa. Resta-nos uma possível dualidade do tipo aditivo e para a qual precisamos, além de estudar melhor o fenômeno, verificar se existe ou não uma "surdez" dos aparelhos de medida. No mais, o que vale é o princípio da certeza de Pitágoras: "O que é, é, e não pode não ser enquanto for".
5 — O Princípio do Fim
Há quem diga que um dos sinais dos últimos tempos será a preocupação excessiva com a pregação da paz. Pode não ser verdadeiro mas é um pensamento sábio. Se existem homens de boa vontade preocupados com a paz, isto significa que vivemos em guerra e visualizamos a autodestruição. Que sejam bem sucedidos os pregadores da paz mas que se diga também que melhor do que defender a paz é não viver em guerra e, assim sendo, não se preocupar com a paz.
A mecânica quântica também vem sendo muito defendida. São inúmeros os artigos referentes à realidade quântica escritos por autores preocupados em defendê-la. Mas a única coisa que conseguem defender é uma série de fórmulas matemáticas. Alguns contentam-se em justificar argumentos de um ou outro dos dois gigantes que há várias décadas duelaram: Einstein e Bohr. Entendem que um dos dois errou mas não sabem qual; e não querem admitir que talvez os dois possam ter acertado. Pois saibam que o que houve não foi propriamente uma disputa mas uma discussão amistosa sob a melhor forma de se construir um campo onde seus sucessores pudessem disputar várias partidas. Os que não entenderam as regras desse jogo chamam a este campo de mecânica quântica. Pois saibam que a mecânica quântica não existe. O que existe chama-se física e esta estuda a natureza real, ainda que admita raciocínios abstratos.
A teoria ondulatória da Luz, com todas as modificações efetuadas e com todas as teorias que se apoiaram no fenômeno onda-luz, chegou ao fim. É chegada a hora de recolher os frutos, e não foram poucos, que permaneceram intactos.
Alguns fanáticos pela teoria quântica hão de dizer que estou blasfemando. Outros continuarão à espera de uma fada madrinha a lhes apontar outra via de raciocínio não absurda, mas coerente com a lógica quântica; e continuarão na procura de suas variáveis escondidas. Existem terceiros que já abandonaram esta ilusão há muito tempo e sabem que fadas madrinhas não existem; sabem também que a tão propalada teoria quântica é um punhado de equações úteis e que portanto insistem em funcionar. Ainda não se sabe porque, mas funcionam. Vamos então continuar utilizando-as; mas que não se diga ser impossível a montanha vir a Maomé. Afinal, nós nem sabemos o que é essa montanha! Sabemos apenas que ela obedece a determinadas equações matemáticas. Nada mais do que isso. Mas a matemática não foi feita para atrapalhar a física nem vice-versa. A matemática jamais modificará a física.
Não me aprofundei na teoria de Schrödinger por motivos óbvios: se ela parte de resultados falsos e acertou o alvo apenas porque é fisicamente tão inexata quanto imprecisa, ou seja, um erro compensou o outro, não há porque nos preocuparmos com ela. Não há duvida que merece uma análise mas deixo isto para quem gosta (mesmo porque, enquanto o quebra-cabeças não estiver completamente montado, esta análise não será simples; e após, será totalmente desnecessária). Também não tenho a resposta para algumas de suas espetaculares predições; mas mesmo que tivesse, não creio que esta lógica parcial pudesse ser simples a ponto de podê-la encaixar neste trabalho.
Em suma: Vamos acordar para a realidade!
* * * * *
Vide também "Teorias Realistas Atuais", uma interessante discussão relativa à incerteza da física moderna e que aconteceu na Lista de Discussão Ciencialist em abril/2000.
Referências:
[1] - Vide Ensaios sobre filosofia e ciência orientais. Série de artigos onde o autor demonstra ser possível, para um ocidental, captar o verdadeiro significado das expressões yin e yang da filosofia oriental e, até mesmo, adaptar tais conceitos ao modo de raciocinar próprio à cultura ocidental.
[2] - Este "princípio" é, na realidade, o teorema XI do princípio unificante da filosofia oriental.
[3] - O leitor poderá encontrar mais detalhes expostos de maneira didática e relativos à esta concepção da luz como campo mutante em "O que são ondas eletromagnéticas?".
[4] - Essa possibilidade é aventada no artigo "O elétron emissor de informações eletromagnéticas".